Sistem Persamaan Linear Dua Variabel Kelas 8 SMP
Sistem persamaan linier dua variabel (SPLDV) – dalam materi matematika kelas 8 SMP ada sebuah materi yang mudah sekali dipahami. Namun bagi anda yang merasa kesulitan memahaminya, bisa melihat penjelasan berikut ini tentang Sistem persamaan linier dua variabel (SPLDV). Pada bab ini ada berbagai system dan konsep perhitungan yang perlu dipahami. Apa saja konsep system persamaan linier dua variabel? Simak ulasannya berikut ini.

Pengertian Persamaan Linear Dua Variabel
Sebenarnya persamaan linear dua variabel pada matematika bisa didefinisikan dengan sebuah persamaan yang mana dalam system tersebut memuat dua buah variabel dan masing masing variabel terdapat hubungan yang punya konsep penyelesaian sama pula. Adapun bentuk umum system persamaan linear dua variabel ialah ax + by = c. Dari bentuk itu, x dan juga y disebut variabel.
Bentuk Umum SPLDV
ax + b = c (Persamaan linear 1 variabel dengan variabelnya x)
px + qy = r (persamaan linear 2 variabel dengan variabelnya x dan y)
Keterangan:
X dan y termasuk variabel pangkat satu.
Lalu a, p, dengan q ialah koefisien.
Sementara untuk b, c dan r merupakan konstanta.
Itulah perbedaan antara keduanya. Jika ada dua ataupun lebih PLDV yang berkaitan antara satu dengan lainnya yang punya satu macam penyelesaian saja, maka itulah yang disebut sebagai SPLDV. Apapun bentuk umum SPLDV ialah sebagai berikut ini:
Bentuk Umum SPLDV 2
Persamaan 1 : px + qy = r
Persamaan 2 : vx + wy = z
Keterangan :
Variabelnya ialah x dan y berpangkat satu.
Sedangkan koefisiennya ialah p, q, w dan v.
Kosntantanya ialah r dan z.
Penyelesaiannya ialah dengan mencri nilai x dengan y.
Biasanya SPLDV digunakan dalam menyelesaikan permasalahan dalam kehidupan sehari hari. Beberapa permasalahan yang yang memerlukn penggunaan Matematika Squad, misalnya menentukan harga barang, menentukn keuntungan pada suatu penjualan, hingga menentukan ukuran sebuah benda. Untuk mencari semua jawaban tersebut, diperlukan langkah-langkah tertentu dalam sistem SPLDV, diantaranya:
- Mengganti pada setiap besaran yang terdapat pada masalah tersebut menggunakan variabel (umumnya dilambangkan pakai huruf ataupun simbol).
- Berikutnya adalah membuat model matematika untuk masalah itu. Adapun model matematikanya akan dirumuskan seperti bentuk umum SPLDV diatas.
- Cari solusi permasalahannya memakai metode penyelesaian SPLDV.
Setelah tahu apa saja langkah langkahnya, silahkan ikuti pembahasan soal dibawah ini.
Soal Latihan SPLDV dan Penyelesainnya
1. Adi ingin melakukan lompat tali. Sementara tali yang dipakainya memiliki panjang 70cm lebih pendek dari tinggi badan adi. Supaya talinya tak tersangkut, adi perlu tali dengan panjang 2 kali panjang tali yang sebelumnya. Sehingga jika di ukur panjang talinya menjadi 30cm lebih panjang dibanding tinggi badan adi. Nah, tentukan berapa tinggi badan adi dan panjang tali yang dipakai untuk bermain lompat tali. Berapa panjang tali supaya talinya tak tersangkut bila di pakai lompat tali adi?
Jawab:
a. Langkah awal yang perlu dilakukan dalam menyelesaikan soal tersebut ialah dengan mengganti seluruh besaran yang terdapa di soal.
X merupakan panjang tali (satuannya cm), sementara y merupakan tinggi badan adi (satuannya juga cm).
b. Langkah selanjutnya adalah dengan membuat model matematika dari permasalah diatas.
Panjang tali ialah 70cm lebih pendek dari panjang tubuh adi, jadi x = y – 70 ataupun –x + y = 70.
Sementara 2 kali panjang tali = 30cm lebih panjang dari tubuh adi, jadi 2x = 30 + y ataupun 2x – y = 30.
Model matematikanya :
Persmaan 1 : -x + y = 70
Persamaan 2 : 2x – y = 30
Metode Penyelesaian SPLDV
1. Metode Grafik
Metode yang pertam ialah metode grafik. Anda bisa menggambarkan grafik dua persamaan diatas. Untuk menggambarnya, anda harus tahu titik potong dari sumbu x dengan sumbu y. menurut contoh diatas, titik potong masing-masing persamaan ialah sebagai berikut ini:


Jadi, didapatkan titik potong kedua garis (x,y) = (100,170). Jadi, dapat di ditentukan panjang tali dengan tinggi badan adi. Yakni 100 cm adalah panjang tali sementara 170 cm merupakan tinggi badan adi.
2. Metode eliminasi
Selanjutnya dengan metode eliminasi. Tujuan dari metode ini ialah menghilangkan atau mengeliminasi satu variabel agar tahu nilai variabel lain. caranya cukup mudah hanya dengan melihat langkah dibawah ini:

Dari gambar diatas juga diketahui jika nilai x nya 100 sedangkan nilai y = 170. Sehingga bisa diketahui jika panjang talinya ialah 100 cm, sementara tinggi badan adi 170 cm.
3. Metode substitusi
Selanjutnya dengan metode substitusi yang tujuannya ialah menggnti nilai variabel dalam persamaan satu dari persamaan lain. Caranya dengan langkah dibawah ini.

Menurut metode substitusi, juga didapat dengan nilai x sebesar 100 sedangkan y = 170. Sehingga bisa di peroleh, tinggi badan adi 170 cm sementara talinya memiliki panjang 100 cm.
4. Metode gabungan
Melihat dari namanya sudah bisa di tebak jika metode yang digunakan ialah gabungan antara metode eliminasi dengan metode substitusi. Langkahnya dengan memakai metode eliminasi lebih dulu untuk mencari nilai x. lalu gantilah variabel x nya dengan nilai yang kamu dapatkan dari metode substitusi tadi guna mencari nilai nilai y nya.

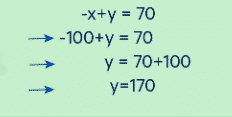
Menurut metode gabungan diatas, didapatkan juga nilai x adalah 100 sementara nilai y = 170. Jadi, panjang talinya ialah 100 cm dan panjang atau tinggi tubuh adi 170 cm.
Jika sudah ketemu semua nilainya, sekarang anda harus tahu panjang tali untuk bermain lompat tali adi supaya tak tersangkut saat digunakan. Panjang talinya harus dua kali dari semula sehingga 2x = 2(100) = 200 cm. Sudah terjawab semua.
Itulah pembahasan tentang Sistem persamaan linier dua variabel (SPLDV). Semoga bermanfaat.
Baca juga: