Pengertian Himpunan Bagian dan Contoh Soal Himpunan Bagian
Himpunan bagian – dibawah ini akan membahas masalah himpunan bagian. Diantaranya pengertian himpunan bagian, contoh himpunan bagian, kemudian himpunan bagian sebuah himpunan, dan contoh soal dari himpunan bagian. Sehingga, kamu bisa mendalami dengan baik pada pembahasan himpunan bagian.
Pengertian Himpunan Bagian
Dalam ilmu matematika, khususnya teori himpunan, sebuah himpunan A merupakan himpunan bagian ataupun subset himpunan B jika A “termuat” dalam B.
Contoh dari Himpunan Bagian.
Agar pemahaman himpunan bagian kamu lebih jelas, perhatikan himpunan berikut.
S = {seluruh siswa kelas VII yang ada di sekolah kamu}
A = {seluruh siswa kelas VIIA yang ada di kelas kamu}
B = {seluruh siswa perempuan VIIA yang ada di kelas kamu}
C = {seluruh siswa laki-laki VIIA yang ada di kelas kamu}
Penjelasan:
Jika melihat dari contoh tersebut, maka diperoleh keterangan dibawah ini:
Himpunan B & himpunan C adalah himpunan bagian himpunan A. Dikarenakan setiap anggota dari himpunan B maupun C adalah anggota himpunan A.
Selanjutnya Himpunan A adalah himpunan bagian himpunan S. Dikarenakan setiap anggota dari himpuna A adalah anggota himpunan S.
Sementara Himpunan B bukan termasuk himpunan bagian himpunan C itu juga sebaliknya. Dikarenakan tak ada anggota dari himpunan B yang termasuk anggota himpunan C atau sebaliknya.
Perhatikanlah diagram Venn yang ada dibawah ini.
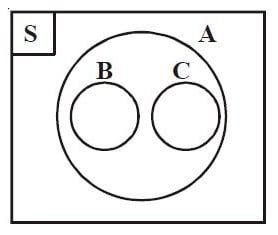
Himpunan B merupakan himpunan bagian himpunan A, dikarenakan anggota B termasuk anggota A juga.
Himpunan A adalah himpunan bagian himpunan S, dikarenakan anggota A anggota S juga.
Sementara himpunan B, bukan termasuk himpunan bagian C ataupun sebaliknya. Dikarenakan anggota B tidak termasuk anggota C, dan sebaliknya. Seperti P = {a, i, e, o, u} & Q = {a, i}, dan anggota R = {n, o, u}. Jadi, Himpunan Q merupakan himpunan bagian himpunan P, dikarenakan setiap anggota Q termasuk juga anggota P, maka bisa ditulis dengan symbol Q Ì P.
Tak semua anggota R adalah angota P, dengan begitu, n ditulis dengan symbol n Ï P. Sehingga, himpunan R bukan termasuk himpunan bagian P, maka ditulis dengan symbol R Ë P.
Kesimpulannya:
Melihat uraian-uraian di atas, maka bisa disimpulkan jika:
Untuk dua himpunan P & Q berarti:
– Himpunan P adalah himpunan bagian Q, maka ditulis P Ì Q, bila setiap anggota P adalah anggota dari himpunan Q.
– Himpunan P tidak termasuk himpunan bagian Q, maka ditulis dengan symbol P Ë Q, bila setiap anggota P tidak merupakan anggota himpunan Q.
Banyaknya Himpunan Bagian dari Sebuah Himpunan
Dalam penjelasan sebelumnya, telah dipelajari jika suatu himpunan adalah himpunan bagian himpunan itu sendiri. Sementara himpunan kosong adalah himpunan bagian suatu himpunan & sekarang akan dipelajari bagaimana cara menentukan banyaknya sebuah himpunan bagian dari sebuah himpunan.
Contoh tentang cara Menyatakan banyaknya suatu himpunan bagian;
Banyaknya suatu himpunan bagian dari sebuah himpunan yang memiliki banyak anggota n dapat ditentukan dengan menggunakan rumus 2n.
Contoh Soal Tentang Himpunan Bagian
Diketahui: suatu himpunan A = {1, 2, 3, 4} maka tentukan banyaknya himpunan bagian himpunan A tersebut.
Penyelesaian:
Banyaknya anggota himpunan A adalah = n(A) = 4, oleh karena itu, banyaknya himpunan bagian A ialah 2.4 = 8.
Itulah pembahasan tentang himpunan bagian. Semoga bermanfaat.
Baca Juga :
- Pengertian Norma Sosial dan Contohnya “Paling Lengkap”
- Rumus Lengkap Pertumbuhan Penduduk (Alami, Migrasi, Total)
- Pengertian, Contoh dan Rumus Barisan Aritmatika beserta Contoh Soal Barisan Aritmatika
